Replicating the Job Importance and Job Satisfaction Latent Class Analysis from the 2017 Survey of Doctorate Recipients with the 2015 and 2019 Cycles
Disclaimer
Working papers are intended to report exploratory results of research and analysis undertaken by the National Center for Science and Engineering Statistics (NCSES). Any opinions, findings, conclusions, or recommendations expressed in this working paper do not necessarily reflect the views of the National Science Foundation (NSF). This working paper has been released to inform interested parties of ongoing research or activities and to encourage further discussion of the topic and is not considered to contain official government statistics.
This research was completed while Dr. Fritz was on academic leave from the University of Nebraska–Lincoln and participating in the NCSES Research Ambassador Program (formerly the Data Analysis and Statistics Research Program) administered by the Oak Ridge Institute for Science and Education (ORISE) and Oak Ridge Associate Universities (ORAU). Any opinions, findings, conclusions, or recommendations expressed in this working paper are solely the author’s and do not necessarily reflect the views of NCSES, NSF, ORISE, or ORAU.
Abstract
Replication and reproducibility of results is a cornerstone of scientific research, as replication studies can identify artifacts that affect internal validity, investigate sampling error, increase generalizability, provide further testing of the original hypothesis, and evaluate claims of fraud. The purpose of the current working paper is to determine whether the five-class, three-response latent class solutions for job importance and job satisfaction found by Fritz (2022) using the 2017 cycle of the Survey of Doctorate Recipients data replicate using data from the 2015 and 2019 cycles. A series of latent class analyses were conducted using the Mplus statistical software, which determined that the five-class, three-response solutions for job importance and job satisfaction were also the best models for the 2015 and 2019 data. In addition, the class prevalences and response probabilities were highly consistent across time, indicating that the interpretation of the latent classes is the same across time as well. All of this gives strong evidence that the 2017 results were successfully replicated in the 2015 and 2019 data, increasing confidence in the original results and also setting the stage for a future longitudinal investigation of the latent classes using latent transition analysis.
Introduction
Background and Rationale
Replication and reproducibility are central tenets of science and scientific inquiry. Put simply, replication is the idea that if it is possible to carry out a research study more than once, then any person who exactly follows the same research protocol as the original study should (within a small margin of error) find the same results as the original study (Fidler and Wilcox 2018), whereas reproducibility is the idea that two people analyzing the same data using the same statistical methods should get the same results. While the concepts of scientific replication and reproducibility are simple, in practice, replication studies often completely or partially fail to replicate the results of previously published scientific studies, leading some to talk about a “replication crisis” in science (Fidler and Wilcox 2018; Pashler and Wagenmakers 2012) or state more strongly that, “It can be proven that most claimed research findings are false” (Ioannidis 2005). Fidler and Wilcox (2018) argue that this “replication crisis” is caused by five interrelated characteristics of the current scientific publication process: (1) the rarity of published replication studies in many fields, (2) the inability to reproduce the statistically significant results of many published studies, (3) a bias towards only publishing scientific studies that report statistically significant effects, (4) a lack of transparency and completeness with regard to sampling and analyses in published studies, and (5) the use of “questionable research practices” such as p hacking in order to obtain significant results. In the U.S. federal statistical system, issues with transparency and reproducibility are important enough that the NCSES tasked the Committee on National Statistics, part of the National Academies of Sciences, Engineering, and Medicine, to produce a consensus study report on the topic (NASEM 2021).
Regardless of the reason, many replication studies fail to reproduce the results of the original study; a consequence of increased focus on replicability is an increased emphasis on the need to reproduce the results from any individual study through the use of one or more replication studies, especially in the social sciences. In general, replication studies fall into two categories: exact replications, which seek to exactly replicate a prior study, and conceptual replications, which seek to determine whether the results of the original study generalize to a new population or context. Regardless of whether a replication study is exact or conceptual, Schmidt (2009) lists five functions of replications studies: (1) control for fraud, (2) control for sampling error, (3) control for artifacts that affect internal validity, (4) increase in generalizability, and (5) further testing of the original hypothesis. In the context of longitudinal survey work, the replication of results at multiple time points increases confidence in the original results and decreases the likelihood that the results at any individual point in time are due solely to artifacts specific to that time point or due to sampling error and measurement error. This increase in confidence, in turn, increases the generalizability of the original results. Ignoring for the moment cases of explicit fraud or data entry and analytic errors, failure to replicate the findings from data collected at one point in time at another point in time could be an indicator of time-specific artifacts or that the effect of interest is changing over time, both of which would require a deeper investigation of the longitudinal structure of the data as a whole.
The purpose of the current working paper is twofold. First is to determine whether the results from Fritz (2022), who found five latent job importance classes and five latent job satisfaction classes using the 2017 cycle of the Survey of Doctorate Recipients (SDR), replicate with the 2015 and 2019 cycle data. Specifically, this paper seeks to rule out the possibility that the results from Fritz (2022) were caused solely by time-specific artifacts (and to a lesser extent, sampling and measurement error) that affected only the 2017 data collection in order to increase confidence in and generalizability of the results of the original study. Second is to lay the groundwork for a future working paper investigating whether individuals move between latent job importance and job satisfaction classes across time (and if so, who moves between classes and in what direction) using latent transition analysis (LTA). Because the first step in conducting an LTA is to determine the latent class structure at each time point, this replication study also fulfills this requirement.
Methods
Data
The current working paper uses the publicly available microdata from the 2015, 2017, and 2019 cycles of the SDR; information about inclusion criteria and sampling are provided in the supporting documentation for the public use files (NCSES 2018, 2019, 2021). To participate in a specific SDR cycle, individuals must have completed a research doctorate in a science, engineering, or health (SEH) field from a U.S. academic institution prior to 1 July two calendar years previous to the current cycle year (e.g., prior to 1 July 2017 for the 2019 cycle). Participants must also be less than 76 years of age and not institutionalized or terminally ill on 1 February of the cycle year. All individuals who were selected to participate in a specific cycle and continued to meet the inclusion criteria were eligible to participate in later cycles, with each cycle’s sample supplemented by individuals who had graduated since the previous cycle. For the 2019 cycle, individuals who did not respond to either the 2015 or 2017 cycles were removed, while 14,564 individuals eligible but not selected for the 2015 cycle were added, and a new stratification design that strengthened reporting for minority groups and small SEH degree fields was utilized. For the final data set of each cycle, missing values were imputed using both logical and statistical methods, and sampling weights were calculated to adjust for the stratified sampling schema; unknown eligibility; nonresponse; and demographic characteristics including gender, race and ethnicity, location, degree year, and degree field.
Participants
Only participants who were asked to respond to the job importance and job satisfaction questions for each cycle were included in the current paper, resulting in final sample sizes of 78,286 individuals for the 2015 cycle, 85,720 individuals for the 2017 cycle, and 80,869 individuals for the 2019 cycle. Table 1 contains the sampling weight–estimated population frequencies by year for gender, physical disability, race and ethnicity, age (in 10-year increments), degree area, whether the participant was living in the United States at the time of data collection, workforce status, and employment sector. Note that these values are based on the reduced samples used for the current analyses and should not be considered official statistics. Although there are some differences across time, in general, the population remained relatively stable in regard to demographics, with the majority of SEH doctoral degree holders for all three cycles identifying as male, White, employed, holding a degree in science, and reporting no physical disability.
Population estimates of Survey of Doctorate Recipients participant characteristics, by selected years: 2015, 2017, and 2019
Note(s):
The values presented here are provided for reference only as they are based on applying the sampling weights to the reduced samples for each collection cycle used for the current project (2015: n = 78,286; 2017: n = 85,720; 2019: n = 80,869) and therefore do not match the official values reported by the National Center for Science and Engineering Statistics. All participants who identified as Hispanic were included in the Hispanic category, and only in the Hispanic category, regardless of whether they also identified with one or more of the racial categories. The Other category included individuals who identified as multiracial.
Source(s):
National Center for Science and Engineering Statistics, Survey of Doctorate Recipients, 2015, 2017, and 2019.
Survey Questions
The current working paper focuses on two SDR questions: “When thinking about a job, how important is each of the following factors to you?” and “Thinking about your principal job held during the week of February 1, please rate your satisfaction with that job’s….” For each question, the participants were asked to rate nine job factors on a 4-point response scale. As in the final models for Working Paper NCSES 22-207 (Fritz 2022), the “somewhat unimportant” and “not important at all” options were combined into a single “unimportant” category and the “somewhat dissatisfied” and “very dissatisfied” options were combined into a single “dissatisfied” category resulting in three response categories for each question. Table 2 shows the sampling weight–estimated population response rates for the three response options for each of the nine job factors for importance and satisfaction. As with Table 1, these values are based on the reduced samples used for the current analyses and should not be considered official statistics. Despite some small variability across time, in general, the response rates for each response option for each job factor were remarkably similar for all three cycles.
Population estimates of response proportions in percentages for importance of and satisfaction with nine job-related factors, by selected years: 2015, 2017, and 2019
Note(s):
The values presented here are provided for reference only as they are based on applying the sampling weights to the reduced samples for each collection cycle used for the current project (2015: n = 78,286; 2017: n = 85,720; 2019: n = 80,869) and therefore do not match the official values reported by the National Center for Science and Engineering Statistics. Percentages may not sum to 100% due to rounding.
Source(s):
National Center for Science and Engineering Statistics, Survey of Doctorate Recipients, 2015, 2017, and 2019.
Analyses and Software
Latent Class Analyses
The current paper uses latent class analysis (LCA), which has the mathematical model (Collins and Lanza 2010)
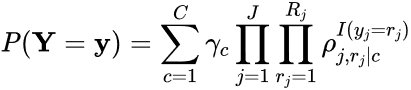
where J is the number of indicators (i.e., job factors, so J = 9), Rj is the number of response options for indicator j (here, Rj = 3), C is the number of latent classes, γc is the prevalence of class c, and ρj,rj|c is the probability of giving response rj to indicator j for a member of class c. While previous work (Fritz 2022) has indicated that there are five job importance latent classes and five job satisfaction latent classes, given that the purpose of the current analyses is to test the veracity of this prior work, multiple models with differing numbers of latent classes were estimated and compared, and the correct number of classes to retain was based on four criteria: (1) percentage decrease in adjusted Bayesian Information Criterion (aBIC) value when an extra latent class was added, (2) solution stability across 1,000 random starts, (3) model entropy, and (4) interpretability of the latent classes.
Software
Sampling weight–estimated population frequencies were computed using PROC SURVEYFREQ with the WEIGHT option in SAS 9.4 (SAS 2021). All LCA models were estimated with Mplus 8.4 (Muthèn and Muthèn 2021) using the maximum likelihood with robust standard errors estimator, treating the indicators as ordered categories (CATEGORICAL) and using 1,000 random starts, each of which was carried through all three estimation stages (STARTS ARE 1000 1000 1000;). Note that while Mplus and PROC LCA (Lanza et al. 2015) give almost identical results (e.g., the results from the 2017 five-class, three-response job importance LCA model in Mplus were identical to the same model in PROC LCA to at least three decimal places), Mplus calculates the aBIC based on the loglikelihood whereas PROC LCA calculates the aBIC based on the G2 statistic, which changes the scaling of the aBIC values. As such, all LCA results for the 2017 SDR cycle reported here have been rerun in Mplus to put the 2017 model aBIC values on the same scale as the 2015 and 2019 model values.
Results
Latent Classes: Job Importance
All LCA models with between one and eight latent classes were fit to the 9 three-response job importance factors separately for the 2015, 2017, and 2019 cycles of SDR data. All models converged normally, although not all 1,000 random starting values converged for the seven- and eight-class models. Table 3 contains the aBIC, percentage decrease in aBIC between models with C + 1 and C classes, entropy, and stability values for each model by year. As described previously, the aBIC values for the 2017 cycle do not match the values from Fritz (2022) because Mplus computes the aBIC values using the loglikelihood rather than G2. Table 3 reveals high consistency in model fit across years. These values indicate that the five-class solution fits the best for all three cycles. For example, adding an additional class reduces the aBIC value by 1.2% or more up through five classes, but adding a sixth latent class only reduces the aBIC value by 0.5% or less for each cycle. In addition, the stability for the five-class solution is highest of the four- through eight-class solutions for all three cycles, and the stability drops substantially for models with more than five classes while the entropy values stay approximately the same.
Model fit indices for job importance latent class analysis models, by selected years: 2015, 2017, and 2019
aBIC = adjusted Bayesian Information Criterion.
Note(s):
Stability is based on 1,000 random starts unless denoted with an asterisk (*), which indicates that not all 1,000 starts converged. When one or more starts failed to converge, stability is based on the number of starts out of 1,000 that did converge. The preferred 5-class solution is shown in bold.
Source(s):
National Center for Science and Engineering Statistics, Survey of Doctorate Recipients, 2015, 2017, and 2019.
The next step is to investigate the interpretation of the five-class solution for the 2015 and 2019 cycles as it is possible that there are five latent classes for each cycle, but that the interpretation of one or more classes is different in the 2017 cycle than the other cycles. The prevalence (i.e., estimated percentage of the population) for each class, as well as the response probabilities for each job factor, of the five-class, three response LCA model are shown in Table 4 by year. As with the previous tables, while the prevalances and response probabilities are not identical for each cycle, Table 4 shows a high level of consistency across years. The largest class for all three cycles is the Everything Is Very Important class whose members have a high probability of rating all nine job factors as “very important.” The second largest class for all three cycles is the Challenge and Independence Are More Important Than Salary and Benefits class whose members are most likely to rate a job’s intellectual challenge, level of independence, and contribution to society as “very important” and the job’s salary and benefits as only “somewhat important.” The Benefits and Salary Are More Important Than Responsibility class is the third largest class for all three cycles, and its members are mostly likely to rate a job’s salary, benefits, and security as “very important” and the job’s level of responsibility as “somewhat important.” The fourth largest class for all three cycles is the Everything Is Somewhat Important class whose members are most likely to rate all nine job factors as “somewhat important.” And the smallest class for each cycle is the Advancement, Security, and Benefits Are Unimportant class whose members are mostly likely to rate a job’s benefits, security, and opportunity for advancement as “unimportant,” although members of this group are likely to rate the job’s location as “very important.” Note that this smallest class is always larger than the 5% rule of thumb for retaining a class (Nasserinejad et al. 2017). Based on this, the five-class, three-response job importance solution reported by Fritz (2022) for the 2017 SDR data does replicate with the 2015 and 2019 cycles of the SDR.
Five-class job importance latent class analysis solution with three response options, by selected years: 2015, 2017, and 2019
Note(s):
Probabilities may not sum to 1.000 due to rounding. Response probabilities greater than or equal to 0.500 are considered salient and are represented in bold. Response probabilities more than twice as large as the next largest probability for that item for a specific year are highlighted in blue.
Source(s):
National Center for Science and Engineering Statistics, Survey of Doctorate Recipients, 2015, 2017, and 2019.
Latent Classes: Job Satisfaction
All LCA models with between one and eight latent classes were fit to the 9 three-response job satisfaction factors separately for the 2015, 2017, and 2019 cycles of SDR data. All models converged normally; again, a small percentage of the 1,000 random starting values did not converge, although just for the eight-class model. Table 5 shows the aBIC, percentage decrease in aBIC between models with C + 1 and C classes, entropy, and stability values for each model by year. As with the model fit indices for job importance, there is a high level of consistency in model fit across cycles for job satisfaction, and stability was 72.2% or higher for the one- through six-class solutions. Unlike the job importance models, however, adding a fifth class reduced the aBIC value by less than 1% for the job satisfaction models. It is important to remember that the decision to include the fifth job satisfaction class in Fritz (2022) was based more on the increased interpretability of the five-class solution compared to the four- and six-class solutions than the improvement in model fit. That is, while inclusion of the fifth class increased model fit modestly, the fifth class improved the separation of the other four classes, making them easier to interpret.
Model fit indices for job satisfaction latent class analysis models, by selected years: 2015, 2017, and 2019
aBIC = adjusted Bayesian Information Criterion.
Note(s):
Stability is based on 1,000 random starts unless denoted with an asterisk (*), which indicates that not all 1,000 starts converged. When one or more starts failed to converge, stability is based on the number of starts out of 1,000 that did converge. The preferred 5-class solution is shown in bold.
Source(s):
National Center for Science and Engineering Statistics, Survey of Doctorate Recipients, 2015, 2017, and 2019.
Investigating the response probabilities and prevalences of the five-class model, shown in Table 6, reveals that the interpretation of the five-class solution is identical for the 2015, 2017, and 2019 cycles, although the rank order of the smaller classes does vary (note that the order of classes in Table 6 is based on the 2017 prevalences). The largest class for all three cycles is the Very Satisfied With Independence, Challenge, and Responsibility class whose members are most likely to rate their satisfaction with their job’s level of independence, intellectual challenge, level of responsibility, and contribution to society as high but are less satisfied with their salary, benefits, and opportunities for advancement. The second largest class for all three cycles is the Very Satisfied With Everything class whose members report being very satisfied with all facets of their current job. While the three smaller classes vary in terms of rank, most likely due to sampling error as the prevalences for these three classes are very similar, the classes themselves are the same across time. Members of the Very Satisfied With Benefits class are most likely to rate their satisfaction with their job’s benefits, salary, and security as “very satisfied,” but only rate their satisfaction with their opportunity for advancement and level of responsibility as “somewhat satisfied.” Members of the Dissatisfied With Opportunities For Advancement class are defined by their high probability of being dissatisfied with their opportunities for advancement in their current job. And the Somewhat Satisfied With Everything class members are mostly likely to rate their satisfaction with all of their job’s facets as “somewhat satisfied.” Based on these results, the five-class, three-response solution was determined to be the correct model for the 2015 and 2019 data, and, as a result, the five-class, three-response job satisfaction solution reported by Fritz (2022) for the 2017 SDR data does replicate with the 2015 and 2019 cycles of the SDR.
Five-class job satisfaction latent class analysis solution with three response options, by selected years: 2015, 2017, and 2019
Note(s):
Probabilities may not sum to 1.000 due to rounding. Response probabilities greater than or equal to 0.500 are considered salient and are represented in bold. Response probabilities more than twice as large as the next largest probability for that item for a specific year are highlighted in blue.
Source(s):
National Center for Science and Engineering Statistics, Survey of Doctorate Recipients, 2015, 2017, and 2019.
Discussion
There are three major take-aways from the results presented here. First, the replication was successful. As shown in Table 3 and Table 5, the fit of the various LCA models is very similar across time, and Table 4 and Table 6 show that the prevalences and response probabilities (and hence, the interpretation) of the latent classes in the 2017 five-class solutions are almost identical to those for the 2015 and 2019 cycles for both job importance and job satisfaction. Perhaps this is unsurprising given the very similar response rates for each cycle shown in Table 2, but all of this indicates that the five-class, three-response LCA solutions for the 2017 SDR data reported by Fritz (2022) do replicate for both job importance and job satisfaction in the 2015 and 2019 cycles of the SDR. While the replication of these five-class solutions provides evidence that these models were not selected solely due to an artifact of the 2017 SDR data, it is important to note that replicating the 2017 results with the 2015 and 2019 data does not rule out all alternative explanations. For example, because the SDR employs a longitudinal, repeated-measures design, with many of the doctoral degree holders who participated in the 2015 cycle also participating in the 2017 and 2019 cycles, it is possible the replication results are due to sampling error, and a different solution would be found with a different sample of doctoral degree holders. In addition, the replication says nothing about whether these five importance and five satisfaction classes are absolute in the sense that what doctoral degree holders in the latter half of the 2010s view as important, and their satisfaction with those job factors may not be the same as for doctoral degree holders in the 1980s or the 2040s. Regardless, replicating the 2017 results strengthens the validity and the generalizability of the original findings (Schmidt 2009).
Second, the replication highlights several findings from Fritz (2022) that, while reported in the original paper, were not as apparent until the results from the 2015, 2017, and 2019 cycles were considered together. For example, for all three cycles, over 70% of respondents were mostly likely to rate opportunities for advancement as “somewhat important” or “unimportant” (Table 4, Classes 2, 3, 4, and 5), but less than 30% of respondents were most likely to rate their satisfaction with their opportunities for advancement at their current job as “very satisfied” (Table 6, Class 2). This would indicate that most respondents were likely to believe their opportunities for advancement at their current job could be improved, and an important area of future research could be investigating why most doctoral degree holders feel this way and what would need to change in order for them to be very satisfied with their opportunities for advancement at their current job.
Another result that stands out in the replication concerns the job location. Table 4 shows that for all three cycles, over 85% of respondents were most likely to rate a job’s location as “very important” (Classes 1, 2, 3, and 5—only members of Class 4 are mostly likely to rate location as “somewhat important”), indicating that job location does not follow the intrinsic or extrinsic divide found by Fritz (2022) for Classes 2 and 3. The same pattern is seen in Table 6 for job satisfaction with members of Class 1, who are mostly likely to rate their satisfaction with only their job’s intrinsic facets as very high, and members of Class 3, who are mostly likely to rate their satisfaction with only their job’s extrinsic facets as very high, both being most likely to rate their satisfaction with their current job’s location as “very satisfied.” This would suggest that a job’s location is neither intrinsic nor extrinsic (or is somehow both). It is also possible that different respondents are interpretating the term “location” differently, with some conceptualizing location as country or state and others conceptualizing job location as a specific neighborhood or distance from their residence (e.g., length of daily commute). As with advancement, future research on doctoral degree holders could seek to better understand how job location relates to satisfaction.
Third, and finally, since the replication involved additional time points using the same sample, some potential longitudinal effects can be examined. For example, the size of some classes appears to systematically change over time, especially for job satisfaction. Most notably, the prevalence of the Satisfied With Independence, Challenge, and Responsibility (Class 1), Dissatisfied With Opportunities For Advancement (Class 4), and Somewhat Satisfied With Everything (Class 5) classes all decrease from 2015 to 2019, whereas the size of the Satisfied With Everything (Class 2) and Satisfied With Benefits (Class 3) classes increase with each additional SDR cycle. While it is tempting to interpret this apparent trend to mean that overall job satisfaction is increasing or that average salary and benefits for doctoral degree holders is increasing, interpreting longitudinal effects in this replication study is problematic for several reasons. The most important issue is that the LCA models presented here do not model or statistically test any longitudinal hypotheses. As noted by Kenny and Zautra (1995), any individual’s score at a specific point in time in repeated-measures data is made up of three types of variability: trait, state, and error. Traits remain stable or change systematically across time; states are nonrandom, time-specific deviations from a trait; and errors are random deviations from a trait. For example, someone who has been in the same job for 10 years might be generally very satisfied with their current job for all 10 years (trait) but was dissatisfied on the day they filled out the SDR because they had an argument with a coworker the previous day (state) and selected “somewhat dissatisfied” because there was no “neither satisfied nor dissatisfied” response option (error).
Longitudinal models that can distinguish between trait, state, and error variability are therefore necessary to test and make conclusions about longitudinal effects. In more exact terms, while the replication of the 2017 solutions with the 2015 and 2019 data indicates that job importance and job satisfaction exhibit a high level of equilibrium that resulted in the same LCA solution at each time point, the replication does not provide any evidence for stability or stationarity of job satisfaction or importance across time. In this context, equilibrium is the consistency of the patterns of covariances and variances between items at a single point in time across repeated measurements (Dwyer 1983), while stability is the consistency of the mean level of a variable across time, and stationarity refers to an unchanging causal relationship between variables across time (Kenny 1979). Investigating whether the average level of satisfaction changed across time or whether the way in which satisfaction changed across time (i.e., the trajectory) differed by latent class would require the use of a latent growth curve model or a growth mixture model, respectively. In addition, the replication does not provide any insight into whether individuals tend to stay in the same class across time or whether individuals change classes, which would require the use of a latent transition model. Based on this, there are numerous longitudinal hypotheses that could be tested in order to gain a more complete understanding of the latent job importance and job satisfaction classes for doctoral degree holders.
References
Collins LM, Lanza ST. 2010. Latent Class and Latent Transition Analysis for Applications in the Social, Behavioral, and Health Sciences. Hoboken, NJ: Wiley.
Dwyer JH. 1983. Statistical Models for the Social and Behavioral Sciences. New York: Oxford University Press.
Fidler F, Wilcox J. 2018. Reproducibility in Scientific Results. In Zalta EN, editor, The Stanford Encyclopedia of Philosophy. Stanford, CA: Metaphysics Research Lab, Stanford University. Available at https://plato.stanford.edu/entries/scientific-reproducibility/#MetaScieEstaMoniEvalReprCris.
Fritz MS; National Center for Science and Engineering Statistics (NCSES). Job Satisfaction versus Job Importance: A Latent Class Analysis of the 2017 Survey of Doctorate Recipients. Working Paper NCSES 22-207. Arlington, VA: National Science Foundation. Available at https://www.nsf.gov/statistics/2022/ncses22207/.
Ioannidis JPA. 2005. Why Most Research Findings Are False. PLoS Medicine 2(8):e124. Available at https://doi.org/10.1371/journal.pmed.0020124.
Kenny DA. 1979. Correlation and Causality. New York: John Wiley & Sons.
Kenny DA, Zautra A. 1995. The Trait-State-Error Model for Multiwave Data. Journal of Consulting and Clinical Psychology 63(1):52–59. Available at https://doi.org/10.1037//0022-006x.63.1.52.
Lanza ST, Dziak JJ, Huang L, Wagner A, Collins LM. 2015. PROC LCA & PROC LTA (Version 1.3.2). [Software]. University Park, PA: Methodology Center, Pennsylvania State University. Available at https://www.latentclassanalysis.com/software/proc-lca-proc-lta/.
Muthèn BO, Muthèn LK. 2021. Mplus (Version 8.4). [Software]. Los Angeles, CA: Muthèn & Muthèn.
Nasserinejad K, van Rosmalen J, de Kort W, Lesaffre E. 2017. Comparison of Criteria for Choosing the Number of Latent Classes in Bayesian Finite Mixture Models. PLoS ONE 12:1–23. Available at https://doi.org/10.1371/journal.pone.0168838.
National Academies of Science, Engineering, and Medicine (NASEM). 2021. Transparency in Statistical Information for the National Center for Science and Engineering Statistics and All Federal Statistical Agencies. Washington, DC: National Academies Press. Available at https://www.nationalacademies.org/our-work/transparency-and-reproducibility-of-federal-statistics-for-the-national-center-for-science-and-engineering-statistics.
National Center for Science and Engineering Statistics (NCSES). 2018. Survey of Doctorate Recipients, 2015. Data Tables. Alexandria, VA: National Science Foundation. Available at https://ncsesdata.nsf.gov/doctoratework/2015/.
National Center for Science and Engineering Statistics (NCSES). 2019. Survey of Doctorate Recipients, 2017. Data Tables. Alexandria, VA: National Science Foundation. Available at https://ncsesdata.nsf.gov/doctoratework/2017/.
National Center for Science and Engineering Statistics (NCSES). 2021. Survey of Doctorate Recipients, 2019. NSF 21-320. Alexandria, VA: National Science Foundation. Available at https://ncses.nsf.gov/pubs/nsf21320/.
Pashler H, Wagenmakers E-J. 2012. Editors’ Introduction to the Special Section on Replicability in Psychological Science: A Crisis of Confidence? Perspectives on Psychological Science 7(6):528–30. Available at https://doi.org/10.1177/1745691612465253.
SAS. 2021. SAS (Version 9.4). Cary, NC: SAS Institute Inc.
Schmidt S. 2009. Shall We Really Do It Again? The Powerful Concept of Replication Is Neglected in the Social Sciences. Review of General Psychology 13(2):90–100. Available at https://doi.org/10.1037/a0015108.
Suggested Citation
Fritz MS; National Center for Science and Engineering Statistics (NCSES). 2022. Replicating the Job Importance and Job Satisfaction Latent Class Analysis from the 2017 Survey of Doctorate Recipients with the 2015 and 2019 Cycles. Working Paper NCSES 22-208. Alexandria, VA: National Science Foundation. Available at https://ncses.nsf.gov/pubs/ncses22208.
Contact Us
NCSES
National Center for Science and Engineering Statistics
Directorate for Social, Behavioral and Economic Sciences
National Science Foundation
2415 Eisenhower Avenue, Suite W14200
Alexandria, VA 22314
Tel: (703) 292-8780
FIRS: (800) 877-8339
TDD: (800) 281-8749
E-mail: ncsesweb@nsf.gov
 An official website of the United States government
An official website of the United States government


